Source code di bawah ini menyelesaikan persamaan difusi 1D yang diaplikasikan dalam penjalaran (transpor, transfer) termal di sebuah batang baja. Lihat bahan ajar mata kuliah Solusi Numerik Persamaan Diferensial. Program dituliskan dalam bahasa pemrograman Python. Program dibuat sederhana agar mudah dibaca dan dimodifikasi oleh pengguna.
Metode Beda Hingga
import numpy as np
# difusi 1D, metode beda hingga, skema implisit
# noinspection PyShadowingNames
def algoritma_thomas(a, b, c, d):
n = len(d)
# matriks asli disimpan ke matriks baru, lokal di sini
cp = c.copy()
bp = b.copy()
dp = d.copy()
# forward sweep
for i in range(1, n):
m = a[i - 1] / bp[i - 1]
bp[i] = bp[i] - m * cp[i - 1]
dp[i] = dp[i] - m * dp[i - 1]
# back substitution
x = np.zeros(n)
x[-1] = dp[-1] / bp[-1]
for i in range(n - 2, -1, -1):
x[i] = (dp[i] - cp[i] * x[i + 1]) / bp[i]
return x
# data
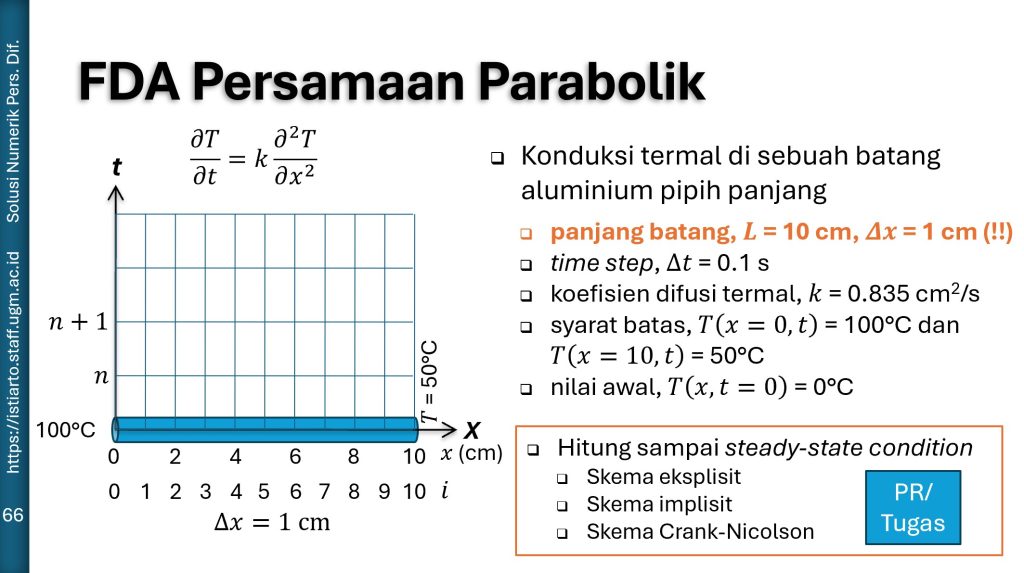
panjang = 10.
k = 0.835
Delta_x = 1.
Delta_t = 0.1
jnode = int(panjang / Delta_x) - 1 # jumlah titik hitung
x = np.linspace(0, panjang, jnode + 2) # posisi titik dari pangkal x=0 s.d. ujung x=10 cm
# variabel skalar dalam contoh kuliah adalah T (temperatur)
# di program ini, variabel temperatur T diganti phi agar tidak rancu dengan variabel waktu t
# syarat awal
phi = np.zeros(jnode) # syarat awal, semua T = 0
# syarat batas
phi_batas_kiri = 100. # syarat batas di pangkal (kiri) T = 100
phi_batas_kanan = 50. # syarat batas di ujung (kanan) T = 50
# koefisien matriks sistem persamaan linear
aki = np.zeros(jnode - 1) # koefisien T_i-1
aka = np.zeros(jnode - 1) # koefisien T_i+1
ai = np.zeros(jnode) # koefisien T_i
rhs = np.zeros(jnode) # konstanta di sisi kanan =
# titik hitung ke-2 s.d. 1 dari batas kanan: i = 1, ..., jnode-2 (karena indeks di python mulai 0)
koef_ki = k * Delta_t / Delta_x / Delta_x
koef_ka = koef_ki
for i in range(1, len(ai) - 1):
aki[i - 1] = -1 * koef_ki
aka[i] = -1 * koef_ka
ai[i] = 1. + koef_ki + koef_ka
rhs[i] = phi[i]
# titik hitung pertama: i = 0 (node bertetangga dengan batas kiri)
i = 0
aka[i] = -1 * koef_ka
ai[i] = 1. + koef_ki + koef_ka
rhs[i] = phi[i] + koef_ki * phi_batas_kiri
# titik hitung paling kanan: i = jnode-1 (node bertetangga dengan batas kanan)
i = len(ai) - 1
aki[i - 1] = -1 * koef_ki
ai[i] = 1. + koef_ki + koef_ka
rhs[i] = phi[i] + koef_ka * phi_batas_kanan
# tulis judul kolom di baris pertama
tulis_teks = " ".join(f"{jarak:9.1f}" for jarak in x)
print(f" {tulis_teks}")
# iterasi phi[i] terhadap waktu t --> t+dt
t = 0.
tulis_teks = " ".join(f"{angka:9.4f}" for angka in phi)
print(f"{t:6.1f} {phi_batas_kiri:9.4f} {tulis_teks} {phi_batas_kanan:9.4f}")
for n in range(1, 201):
t = n * Delta_t
phi = algoritma_thomas(aki, ai, aka, rhs)
if (t % 1) == 0:
tulis_teks = " ".join(f"{angka:9.4f}" for angka in phi)
print(f"{t:6.1f} {phi_batas_kiri:9.4f} {tulis_teks} {phi_batas_kanan:9.4f}")
rhs[0] = phi[0] + koef_ki * phi_batas_kiri
for i in range(1, len(rhs) - 1):
rhs[i] = phi[i]
rhs[len(rhs) - 1] = phi[len(rhs) - 1] + koef_ka * phi_batas_kanan
print("selesai")
Metode Volume Hingga
import numpy as np
# TUGAS Makul SNPD
# Difusi 1D, skema implisit, metode volume hingga
# noinspection PyShadowingNames
def algoritma_thomas(a, b, c, d):
n = len(d)
# matriks asli disimpan ke matriks baru, lokal di sini
cp = c.copy()
bp = b.copy()
dp = d.copy()
# forward sweep
for i in range(1, n):
m = a[i - 1] / bp[i - 1]
bp[i] = bp[i] - m * cp[i - 1]
dp[i] = dp[i] - m * dp[i - 1]
# back substitution
x = np.zeros(n)
x[-1] = dp[-1] / bp[-1]
for i in range(n - 2, -1, -1):
x[i] = (dp[i] - cp[i] * x[i + 1]) / bp[i]
return x
# data
panjang = 10. # cm
Gamma = 0.835 # cm^2/s
Delta_x = 1. # cm
Delta_t = 0.1 # s
diameter = 0.6 # cm
luas = 0.25 * np.pi * diameter ** 2
Delta_V = luas * Delta_x
jmlvc = int(panjang / Delta_x) # jumlah volume kontrol
Delta_x = panjang / jmlvc # Delta_x dihitung ulang untuk penyesuaian dengan jumlah volume kontrol
x1 = np.arange(Delta_x/2, panjang, Delta_x) # jarak/posisi volume kontrol
x = np.concatenate(([0.], x1, [10.])) # jarak pangkal (x=0), volume kontrol, ujung (x=10)
# syarat awal
phi = np.zeros(jmlvc)
# syarat batas
phi_kiri = 100. # der C
phi_kanan = 50. # der C
# koefisien matriks tridiagonal
aW = np.zeros(jmlvc - 1) # diagonal bawah: jumlah koefisien adalah jumlah vk-1
aE = np.zeros(jmlvc - 1) # diagonal atas: jumlah koefisien adalah jumlah vk-1
aP = np.zeros(jmlvc) # diagonal utama: jumlah koefisien adalah jumlah vk
rhs = np.zeros(jmlvc) # konstanta di sisi kanan tanda kesamaan "="
# volume kontrol 2, 3, ..., jmlvc-1: i=1, 2, ..., jmlvc-2
koef_W = Gamma * luas * Delta_t / Delta_x / Delta_V
koef_E = koef_W
for i in range(1, jmlvc - 1):
aW[i - 1] = -1 * koef_W
aE[i] = -1 * koef_E
aP[i] = koef_W + koef_E + 1.
rhs[i] = phi[i]
# volume kontrol 1: i=0
koef_kiri = Gamma * luas * Delta_t / (Delta_x / 2) / Delta_V
aE[0] = -1 * koef_E
aP[0] = koef_kiri + koef_E + 1.
rhs[0] = phi[0] + koef_kiri * phi_kiri
# volume kontrol paling kanan: i=jmlvc-1
koef_kanan = Gamma * luas * Delta_t / (Delta_x / 2) / Delta_V
aW[jmlvc - 2] = -1 * koef_W
aP[jmlvc - 1] = koef_W + koef_kanan + 1.
rhs[jmlvc - 1] = phi[jmlvc - 1] + koef_kanan * phi_kanan
# iterasi phi[i] terhadap waktu t --> t+dt
t = 0.
tulis_teks = " ".join(f"{angka:9.1f}" for angka in x) # Mengubah angka x menjadi teks
print(f" {tulis_teks}") # Menuliskan posisi volume kontrol di baris pertama
tulis_teks = " ".join(f"{angka:9.4f}" for angka in phi) # Mengubah angka phi menjadi teks
print(f"{t:6.1f} {phi_kiri:9.4f} {tulis_teks} {phi_kanan:9.4f}") # Menuliskan nilai awal phi
for n in range(1, 201): # Menghitung phi pada waktu t+Delta_t
t = n * Delta_t
phi = algoritma_thomas(aW, aP, aE, rhs) # Penyelesaian persamaan linear, matriks tridiagonal
if (t % 1) == 0: # Mencetak hasil hitungan tiap detik
tulis_teks = " ".join(f"{angka:9.4f}" for angka in phi)
print(f"{t:6.1f} {phi_kiri:9.4f} {tulis_teks} {phi_kanan:9.4f}")
rhs[0] = phi[0] + koef_kiri * phi_kiri
for i in range(1, jmlvc - 1):
rhs[i] = phi[i]
rhs[jmlvc - 1] = phi[jmlvc - 1] + koef_kanan * phi_kanan
print("selesai")
