i s t i a r t o

Author: sekti

  • Kursus HEC-RAS Oktober 2012

    Memenuhi permintaan beberapa peminat, JTSL FT UGM menyelenggarakan kursus pemakaian HEC-RAS. Kursus akan diselenggarakan pada: Jumat s.d. Minggu, 19-21 Oktober 2012, di Kampus JTSL FT UGM.

    Informasi rinci tentang kursus dapat diperoleh melalui kontak email kepada Dwi Haryati di alamat dwi@tsipil.ugm.ac.id.

  • Respon yang lambat terhadap comment

    Hari-hari ini, beberapa respon saya terhadap comment yang dituliskan pada situs/blog ini lambat. Beberapa comment bahkan terlambat saya approve. Saya mohon maaf. Salah satu penyebab keterlambatan adalah adanya spam yang masuk ke situs ini melalui comment. Jumlah spam terasa meningkat akhir-akhir ini. Saya membutuhkan waktu untuk memilahnya dan ada comment yang kadang terselip di antara spam.

    Mohon kesabaran rekan-rekan apabila merasa comment Anda lambat muncul dan respon baru muncul setelah beberapa hari.

  • Nilai Ujian Remedi Matematika I (2 Agustus 2012)

    Akhirnya, saya telah menetapkan nilai ujian remedi Matematika I (2012). Ada usulan dari mahasiswa yang disampaikan kepada saya untuk memberikan nilai B kepada semua peserta ujian. Saya terpaksa tidak dapat memenuhi usulan tersebut mengingat hal itu 1) menghilangkan faktor keadilan, yaitu menafikkan adanya mahasiswa yang telah bekerja keras dan mahasiswa yang tidak bersungguh-sungguh mengikuti ujian, serta 2) menyamakannya dengan hukuman pada kasus dosen yang terlambat menyerahkan nilai ujian, padahal saya tidak terlambat.

    Dengan semangat tetap membantu mahasiswa, saya tetapkan nilai dengan mengacu pada batas bawah nilai yang cukup rendah pada setiap tingkat nilai, yaitu:

     

    • nilai angka rata-rata ditambah satu kali simpangan baku untuk nilai B,
    • nilai angka rata-rata dikurangi setengah simpangan baku untuk nilai C,
    • nilai angka satu untuk nilai D.

    Sebaran jumlah mahasiswa pada masing-masing nilai adalah sebagai berikut: 14 (B), 29 (C), 22 (D), dan 4 (E). “IP mata kuliah” adalah 1.77. Sangat rendah memang. Saya sadar, mahasiswa kecewa. Tetapi saya lebih kecewa lagi. Semoga pada tahun depan nilai tidak lagi seperti ini. Tayangan grafis nilai saya sertakan di bawah ini.

    image

  • Nilai Ujian Matematika I (Remedi 2012)

    Hari ini dilakukan rapat membahas nilai ujian remedi tahun akademik 2011-2012. Nilai Matematika I belum saya serahkan kepada Jurusan. Ada yang mengusik benak saya setelah mencermati hasil pekerjaan ujian mahasiswa. Jumlah soal ujian 20 dan setiap soal saya beri bobot sama. Pemberian nilai dilakukan secara “strict”. Nilai 1 jika benar dan 0 jika salah. Saya tayangkan nilai setiap mahasiswa pada gambar di bawah ini.

    image

    Bagi saya, nilai tersebut sangat mengecewakan. Terlalu rendah, jauh dari nilai yang saya harapkan. Apa yang terjadi? Salah siapa atau apa yang salah? Plis, beri tahu pendapat atau komentar Anda, khususnya Anda mahasiswa peserta ujian. Terus… bagaimana saya harus mentransfer nilai tersebut menjadi nilai B-C-D-E (tidak ada nilai A pada ujian remedi)? Plis, beri saya saran. Eni sejessyen is welkam. Saya tunggu sampai Senin, 13-8-2012, pagi.

  • Model 3D Aliran di Saluran Terbuka

    Salah satu topik dalam disertasi doktor saya beberapa tahun yang lalu adalah model tiga-dimensi aliran di saluran terbuka. Saya memakai metode volume hingga (finite volume method) untuk menyelesaikan persamaan aliran di saluran terbuka. Model turbulen yang saya pilih adalah model k-ε. Source code program dituliskan dalam Fortran. Anda yang tertarik mempelajari model yang saya susun, silakan mengunduh naskah Bab IV disertasi saya yang memaparkan tentang penyusunan model 3D ini. Bagi yang berminat untuk menyusun program aplikasi model 3D aliran di saluran terbuka, saya akan sangat senang untuk berdiskusi dan saling bertukar pengetahuan dan pengalaman.

    Bab IV Disertasi

     

  • HEC-RAS: Sungai Berkelok

    Ada pertanyaan dari salah seorang pembaca website ini mengenai cara memodelkan sungai berkelok. Saya cuplik pertanyaan dia (saya ubah kalimat dia agar lebih mudah kita baca): “Saya ingin bertanya tentang sungai yg berbelok belok. Bagaimanakah cara memodelkannya dalam HEC RAS? Apakah HEC RAS mengganggap alur sungai seperti itu sebagai sungai lurus?”

    HEC-RAS mengenali alinemen alur sungai dari data panjang ruas antara suatu river station dengan river station di sisi hilirnya atau, dalam bahasa sederhana, jarak antara suatu tampang lintang (cross section) dengan tampang lintang berikutnya di sisi hilir tampang lintang tersebut. HEC-RAS meminta tiga data panjang ruas, yaitu panjang ruas bantaran kiri, panjang ruas alur utama, dan panjang ruas bantaran kanan. Panjang ruas ini bukan panjang fisik geometri sungai, tetapi jarak tempuh aliran di ketiga bagian tampang tersebut. Saya berikan satu contoh di bawah ini.

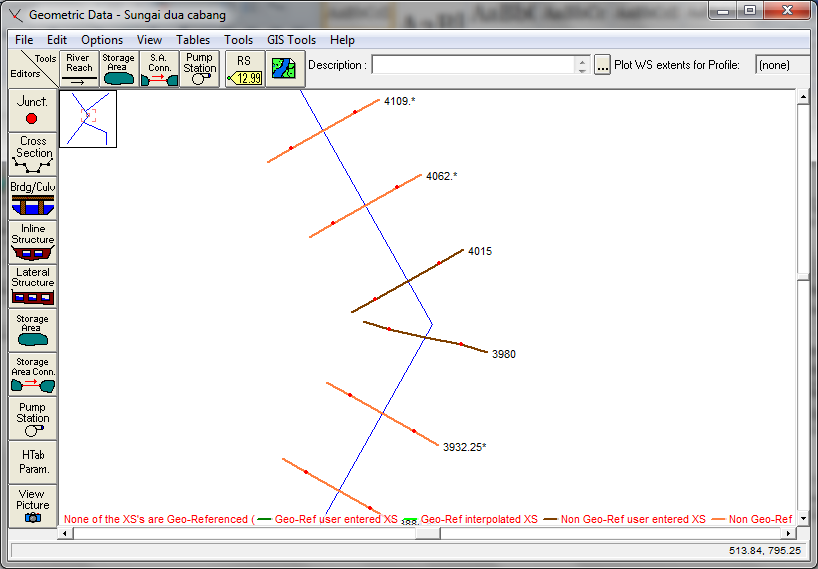
    Sketsa alur sungai pada gambar pertama menunjukkan bahwa alur sungai antara RS 4015 dan RS 3980 berbelok ke kanan. Untuk memberitahukan fitur kelokan ini kepada HEC-RAS, kita masukkan data jarak yang ditempuh aliran dari RS 4015 ke RS 2980 pada bagian bantaran kiri, alur utama, dan bantaran kanan. Data ini kita masukkan pada layar editor Cross Section Data (lihat gambar kedua). Pada isian Downstream Reach Lengths, kita masukkan jarak tempuh aliran di bantaran kiri sebagai data LOB (62.5 m), jarak tempuh aliran di alur utama sebagai data Channel (35 m), dan jarak tempuh aliran di bantaran kanan sebagai data ROB (7.5 m).

    Bagaimanakah cara kita mengukur jarak tempuh aliran LOB, Channel, ROB? Saran saya, jarak ini kita tentukan dengan mencermati situasi di lapangan. Langkah awal, dapat saja kita memakai gambar situasi. Namun, kita perlu memeriksa lapangan untuk mendapatkan informasi yang lebih baik. Kita perlu pula memperhatikan besaran debit aliran yang ingin kita simulasikan. Tidak tertutup kemungkinan bahwa jarak tempuh aliran LOB, Channel, ROB berbeda pada nilai debit aliran yang berlainan.

    Saya perlu menekankan bahwa jarak LOB, Channel, ROB adalah jarak tempuh aliran, bukan jarak fisik geometri antara kedua river station. Kurang tepat apabila LOB diisi dengan data jarak antar titik data paling kiri atau titik paling kiri alur utama di RS 4015 dan RS 3980. Demikian pula, kurang tepat apabila Channel diisi dengan data jarak antar titik tengah kedua RS tersebut, serta kurang tepat pula apabila ROB diisi dengan data jarak antar titik paling kanan atau titik paling kanan alur utama kedua RS tersebut.

    Kesalahan yang fatal, tetapi pernah saya temui, adalah sebuah model alur sungai berkelok-kelok (tampak pada gambar river network pada layar editor Geometric Data), tetapi data LOB, Channel, ROB pada Downstream Reach Length berisi nilai yang sama. Model tetap “jalan” dan memberikan hasil. Tetapi tentu saja HEC-RAS memodelkan sungai berkelok-kelok tersebut sebagai sungai lurus!

  • UTS Matematika I (12 April 2012)

    Di bawah ini adalah tautan untuk mengunduh file soal dan penyelesaiannya. File penyelesaian adalah revisi dari file yang pernah saya tayangkan pada 16-April-2012.  Ada tambahan gambar sketsa pada penyelesaian soal nomor 20. Apabila Anda masih menemukan kesalahan pada penyelesaian soal UTS tersebut, harap memberitahukannya kepada saya melalui comment di bawah post ini.

    Soal UTS Matematika I 12Apr12 (119 KB)
    Penyelesaian Soal UTS Matematika I 12Apr12 (416 KB)

  • Kuis Matematika I (19 Maret 2012)

    Kuis kedua Matematika I pada Semester Genap 2011-2012 diselenggarakan pada Senin, 19 Maret 2012. Kuis diikuti oleh 64 mahasiswa. Berbeda dengan kuis pertama pada 5 Maret 2012 yang lalu, kali ini banyak mahasiswa yang dapat mengerjakan soal-soal kuis dengan baik dan benar. Penyelesaian soal kuis dapat diunduh dari tautan di bawah ini.

    Penyelesaian Kuis Matematika I 19Mar12

  • Kuis Matematika I (5 Maret 2012)

    Kuis pertama Matematika I pada Semester Genap 2011-2012 diselenggarakan pada Senin, 5 Maret 2012. Kuis diikuti oleh 60 mahasiswa. Banyak mahasiswa yang tidak dapat mengerjakan soal-soal kuis dengan baik dan benar. Penyelesaian soal kuis dapat diunduh dari tautan di bawah ini.

    Penyelesaian Kuis Matematika I 05Mar12

  • CFD di Bidang Hidraulika: Model Aliran dan Transpor Massa

    Topik spesial S2: 3 sks, Semester II TA 2011-2012, teori dan praktik.

    Dosen: Istiarto

    Disarankan bagi mahasiswa yang mengikuti topik ini untuk mendalami topik ini lebih lanjut dan menggabungkannya dengan tesis.

    Tidak ada syarat bahwa mahasiswa sudah menguasai MatLab. Pengantar pemakaian MatLab akan diberikan pada saat kuliah. Mahasiswa belajar memakai MatLab sambil praktek membuat program aplikasi model aliran dan transpor konveksi-difusi.

    Tujuan

    Mahasiswa memahami dan menguasai metode dan teknik komputasi di bidang hidrodinamika, serta mampu melakukan analisis aliran (free surface flow) dan transpor sedimen-polutan dengan memakai model matematika.

    Pada akhir kuliah, mahasiswa berhasil membuat program transpor massa konveksi-difusi satu dimensi dan program aliran saluran terbuka.

    Silabus

    Pengantar CFD di bidang hidraulika dan transpor massa (sedimen-polutan). Persamaan aliran fluida dan transpor massa (3D): konservasi massa, konservasi momentum, dan konservasi energi. Turbulen dan model turbulen. Persamaan transpor difusi-konveksi. Metode volume hingga untuk penyelesaian persamaan transpor difusi. Metode volume hingga untuk penyelesaian persamaan transpor difusi-konveksi: upwind differencing scheme, power-law scheme, QUICK scheme. Syarat batas (boundary conditions). Metode volume hingga untuk penyelesaian persamaan aliran: SIMPLE scheme. Computational grids: staggered, non-staggered grids. Algoritma penyelesaian persamaan kerja: tridiagonal matrix algorithm. Praktek pembuatan model transpor konvektif-difusif dengan spreadsheet (MSExcel) dan MatLab.

    Referensi

    Bahan Kuliah (class notes) disediakan, dapat diunduh di https://istiarto.staff.ugm.ac.id/pada minggu pertama masa kuliah.

    Versteeg H.K., W. Malalasekera, 1995, An Introduction to Computational Fluid Dynamics, Longman, Essex, England.

    Agenda Tatap Muka (Kuliah)

    Minggu

    Materi

    Keterangan

    I

    Pengantar CFD.

    ·         Pengenalan CFD.

    ·         Struktur CFD: pre-processor, solver, post-processor.

    Ruang kelas.

    Presentasi contoh CFD, demonstrasi aplikasi CFD.

    II

    Aliran dan transpor massa.

    ·         Aliran di saluran terbuka.

    ·         Aliran turbulen, laminar.

    ·         Transpor massa.

    Laboratorium Hidraulika.

    Demonstrasi aliran di saluran terbuka, aliran turbulen dan laminar (Osborn-Reynolds apparatus).

    Demonstrasi transpor massa: difusi, konveksi-difusi.

    III

    Persamaan aliran dan transpor.

    ·         Persamaan konservasi: massa, momentum, energi.

    ·         Persamaan aliran dan transpor dalam bentuk integral dan diferensial.

    ·         Turbulen dan model turbulen.

    Ruang kelas (mhs membawa komputer).

    Mahasiswa memahami arti fisik setiap suku dalam persamaan aliran dan transpor.

    Mahasiswa melakukan penyusunan persamaan aliran dan transpor.

    Mahasiswa menganalisis data pengukuran kecepatan aliran (data disediakan).

    IV

    Difusi permanen satu dimensi.

    ·         Persamaan konveksi-difusi 1D.

    ·         Persamaan difusi 1D.

    Metode volume hingga.

    ·         Pengantar metode volume hingga.

    ·         Diskritisasi persamaan difusi 1D dengan metode finite volume.

    ·         Syarat batas.

    Ruang kelas.

    Mahasiswa memahami persamaan difusi satu dimensi dan menguasai teknik penyelesaian persamaan difusi dengan metode volume hingga.

    Mahasiswa mempraktekkan diskritisasi persamaan difusi 1D.

    Mahasiswa mampu melakukan diskritisasi persamaan difusi 1D dengan metode volume hingga.

    V

    Metode volume hingga untuk penyelesaian persamaan difusi 1D.

    ·         Penyelesaian persamaan difusi 1D dengan bantuan spreadsheet (MSExcel).

    Ruang kelas (mhs membawa komputer).

    Mahasiswa mampu melakukan pemrograman persamaan difusi 1D dengan spreadsheet (MSExcel).

    VI

    Metode volume hingga untuk penyelesaian persamaan konveksi-difusi 1D.

    ·         Persamaan konveksi-difusi.

    ·         Berbagai metode diskritisasi.

    ·         Skema upwind.

    ·         Skema power law.

    ·         Skema QUICK

    ·         Syarat batas.

    ·         Difusi numerik (false diffusion).

    ·         Pemrograman dengan spreadsheet (MSExcel).

    Ruang kelas.

    Mahasiswa memahami syarat batas, mampu menetapkan syarat batas, mengerti arti fisiknya, serta memahami keterbatasan/kesalahan model.

    Mahasiswa diberi tugas/PR untuk membuat program konveksi-difusi 1D dengan spreadsheet (MSExcel).

    VII

    Review dan diskusi.

    Ruang kelas (mhs membawa komputer).

    Presentasi dan diskusi model transpor konveksi-difusi yang dibuat dengan spreadsheet (MSExcel).

    VIII

    Ujian Tengah Semester.

    Ujian lisan, presentasi model transpor 1D koveksi-difusi.

    IX

    Metode volume hingga untuk penyelesaian persamaan konveksi-difusi 1D.

    ·         Pengantar MatLab.

    ·         Pemrograman difusi 1D dengan MatLab.

    ·         Pemrograman konveksi-difusi 1D dengan MatLab.

    Ruang kelas (mhs membawa komputer).

    Mahasiswa mampu memakai MatLab untuk membuat program konveksi-difusi 1D.

    Mahasiswa diberi tugas/PR untuk menyelesaikan program konveksi-difusi 1D dengan MatLab.

    X

    Review dan diskusi.

    Ruang kelas (mhs membawa komputer).

    Presentasi dan diskusi tugas/PR program konveksi-difusi 1D dengan MatLab.

    XI

    Metode volume hingga untuk penyelesaian persamaan aliran permanen.

    ·         Review persamaan aliran di saluran terbuka (open channel flow).

    ·         Diskritisasi persamaan momentum.

    ·         Grid: staggered grids.

    Ruang kelas.

    Mahasiswa memahami dan dapat melakukan diskritisasi persamaan momentum, serta mampu menyusunnya menjadi persamaan yang siap untuk diselesaikan.

    XII

    Metode volume hingga untuk penyelesaian persamaan aliran permanen.

    ·         Syarat batas.

    ·         Skema SIMPLE.

    ·         Grid: staggered grid.

    Ruang kelas (mhs membawa komputer).

    Mahasiswa memahami dan dapat melakukan hitungan tekanan dan kecepatan aliran (pressure and velocity fields).

    XIII

    Metode volume hingga untuk penyelesaian persamaan aliran permanen.

    ·         Penyusunan program dengan MatLab.

    Ruang kelas (mhs membawa komputer).

    Mahasiswa mampu membuat program aliran permanen dengan MatLab.

    XIV

    Metode penyelesaian persamaan dengan tridiagonal matrix algorithm (TDMA).

    Ruang kelas (mhs membawa komputer).

    Mahasiswa memahami dan mampu melakukan penyusunan persamaan-persamaan hasil diskritisasi persamaan aliran permanen dan mampu menyelesaikannya dengan metode TDMA.

    XV

    Review dan diskusi.

    Ruang kelas (mhs membawa komputer).

    Presentasi dan diskusi tentang diskritisasi persamaan aliran, serta penyelesaian persamaan dengan TDMA.

    XVI

    Ujian Akhir Semester.

    Ujian lisan, presentasi model aliran.