Terima kasih atas kunjungan Anda
Terima kasih atas kunjungan Anda
Semoga informasi di situs ini bermanfaat bagi Anda.
Saya sangat menghargai setiap komentar, usulan, saran, pertanyaan.
Silakan mengirimkannya melalui email ke istiarto@ugm.ac.id.
Source Code Kontur Konveksi-Difusi
Source code di bawah ini memplotkan kontur konsentrasi polutan yang diperoleh dari penyelesaian analitik persamaan transpor konveksi-difusi di sungai. Lihat bahan ajar mata kuliah Dinamika Aliran dan Transfer Massa. Program dituliskan dalam bahasa pemrograman Python. Program dibuat sederhana agar mudah dibaca dan dimodifikasi oleh pengguna.
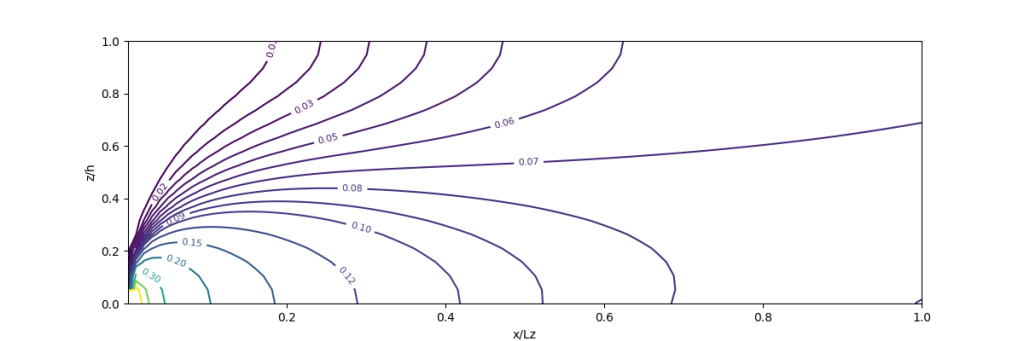
Konveksi-Difusi Vertikal (di Near-field Zone)
Exercise 8B
import numpy as np
import matplotlib.pyplot as plt
# Dinamika Aliran dan Transfer Massa
# Konveksi-difusi vertikal
# Exercise 8B
# data
Q = 103.7
U = 1.05
B = 90.6
h = 1.09
ustar = 0.07
Sf = 0.0005
T = 10.
C = 10.
Qu = 0.5
Tu = 20.
Cu = 30.
xsi = 0.4
# hitungan
A = B * h
etz = 0.067 * h * ustar
Lz = xsi * U * h * h / etz
tz = Lz / U
nx = 100
nz = 20
# dx = Ly / nx
# dz = h / nz
print("Ly ", Lz, "m")
print("ty", tz, "s")
x = np.linspace(0.01, Lz, nx)
z = np.linspace(0.0, h, nz)
c = np.zeros((len(x), len(z)), dtype=float)
Gu = Cu * Qu
i = 0
for xc in x:
j = -1
for zc in z:
j = j + 1
c[i, j] = Gu / B / np.sqrt(4 * np.pi * etz * xc * U) * np.exp(-1. * zc * zc * U / (4. * etz * xc))
zz = zc - 2 * h
c[i, j] = c[i, j] + Gu / B / np.sqrt(4 * np.pi * etz * xc * U) * np.exp(-1. * zz * zz * U / (4. * etz * xc))
zz = zc
c[i, j] = c[i, j] + Gu / B / np.sqrt(4 * np.pi * etz * xc * U) * np.exp(-1. * zz * zz * U / (4. * etz * xc))
i = i + 1
tulis_teks = " ".join(f"{val:7.4f}" for val in z)
print(f" {tulis_teks}")
ii = 0
for row in c:
tulis_teks = " ".join(f"{val:7.4f}" for val in row)
print(f"{x[ii]:9.4f} {tulis_teks}")
ii = ii + 1
print("Selesai hitungan konsentrasi")
# plot kontur konsentrasi
x = x / Lz
z = z / h
print("cmin, cmaks ", np.min(c), np.max(c))
zi, xi = np.meshgrid(z, x)
kontur1 = ([0.001])
kontur2 = np.linspace(0.01, 0.20, 20) # nilai-nilai c yg akan di-kontur-kan
kontur3 = ([0.25, 0.3, 0.4, 0.5, 0.6]) # nilai-nilai c yg akan di-kontur-kan
kontur = np.hstack((kontur1, kontur2, kontur3))
plt.figure(figsize=(12, 6))
plot = plt.contour(xi, zi, c, levels=kontur, cmap='viridis')
plt.xlabel('x/Ly', fontsize=14)
plt.ylabel('z/h', fontsize=14)
plt.clabel(plot, inline=1, fontsize=8)
plt.savefig('kontur_kondif_vertikal.png')
plt.show()
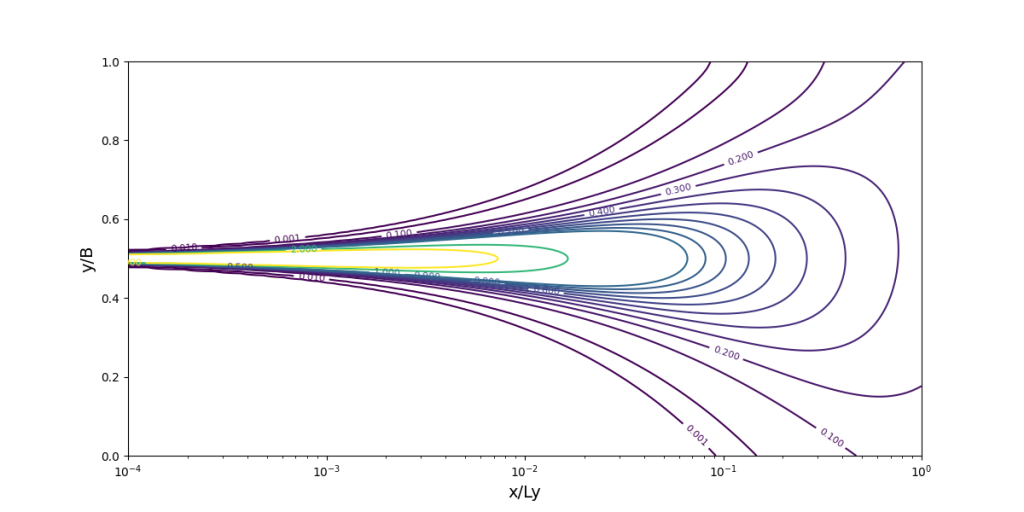
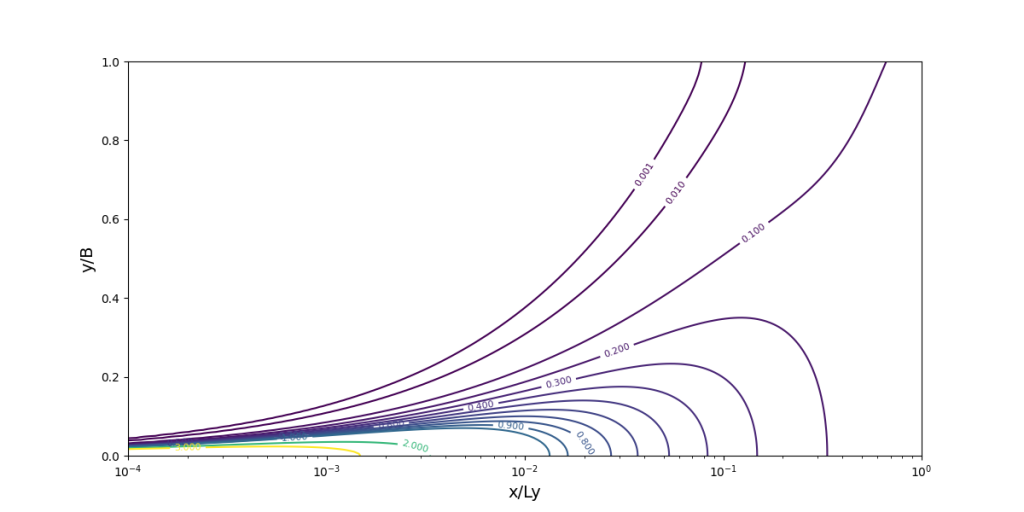
Konveksi-Difusi Transversal (di Mid-field Zone)
Exercise 8C
import numpy as np
import matplotlib.pyplot as plt
# Dinamika Aliran dan Transfer Massa
# Konveksi-difusi transversal
# Exercise 8C
# data
Q = 103.7
U = 1.05
B = 90.6
h = 1.09
ustar = 0.07
Sf = 0.0005
Qu = 0.5
Cu = 30.
# Posisi source
# y0 = B / 2.
y0 = 0.
if y0 == 0.0:
xsi = 0.5
else:
xsi = 0.1
print("xsi", xsi)
# hitungan
A = B * h
ety = 0.6 * h * ustar
print("ety", ety)
Ly = xsi * U * B * B / ety
ty = Ly / U
Ly = np.round(Ly / 1000, 0) * 1000.
ty = np.round(ty / 3600, 0) * 3600.
print("Ly ", Ly, "m", Ly / 1000, "km")
print("ty", ty, "s", ty / 3600, "jam")
nx = 200
ny = 200
x = np.logspace(-4, 0, nx)
y = np.linspace(B, 0., ny)
c = np.zeros((len(y), len(x)), dtype=float)
Gu = Cu * Qu
j = 0
for col in x:
# xc = np.power(10, col) * Ly
xc = col * Ly
koef = Gu / h / np.sqrt(4 * np.pi * ety * xc * U)
i = -1
for row in y:
i = i + 1
yc = row - y0 # original source
c[i, j] = koef * np.exp(-1. * yc * yc * U / (4. * ety * xc))
yc = row - (2. * B - y0) # image source kiri
c[i, j] = c[i, j] + koef * np.exp(-1. * yc * yc * U / (4. * ety * xc))
yc = row - y0 # image source kanan
c[i, j] = c[i, j] + koef * np.exp(-1. * yc * yc * U / (4. * ety * xc))
j = j + 1
tulis_teks = " ".join(f"{val:7.4f}" for val in x)
print(f" {tulis_teks}")
tulis_teks = " ".join(f"{val * Ly / 1000:7.4f}" for val in x)
print(f" {tulis_teks}")
ii = 0
for row in c:
tulis_teks = " ".join(f"{val:7.4f}" for val in row)
print(f"{y[ii]:9.4f} {tulis_teks}")
ii = ii + 1
print("Selesai hitungan konsentrasi")
# plot kontur konsentrasi
y = y / B
print("cmin, cmaks ", np.min(c), np.max(c))
xi, yi = np.meshgrid(x, y)
# nilai-nilai kontur yang akan diplotkan
kontur1 = np.linspace(0.001, 0.01, 2)
kontur2 = np.linspace(0.1, 1, 10)
kontur3 = ([2.0, 3.0])
kontur = np.hstack((kontur1, kontur2, kontur3))
plt.figure(figsize=(12, 6))
plot = plt.contour(xi, yi, c, levels=kontur, cmap='viridis')
plt.xscale('log')
plt.xlabel('x/Ly', fontsize=14)
plt.ylabel('y/B', fontsize=14)
plt.clabel(plot, inline=1, fontsize=8)
plt.savefig('kontur_kondif_transversal.png')
plt.show()
Source Code Difusi 1D
Source code di bawah ini menyelesaikan persamaan difusi 1D yang diaplikasikan dalam penjalaran (transpor, transfer) termal di sebuah batang baja. Lihat bahan ajar mata kuliah Solusi Numerik Persamaan Diferensial. Program dituliskan dalam bahasa pemrograman Python. Program dibuat sederhana agar mudah dibaca dan dimodifikasi oleh pengguna.
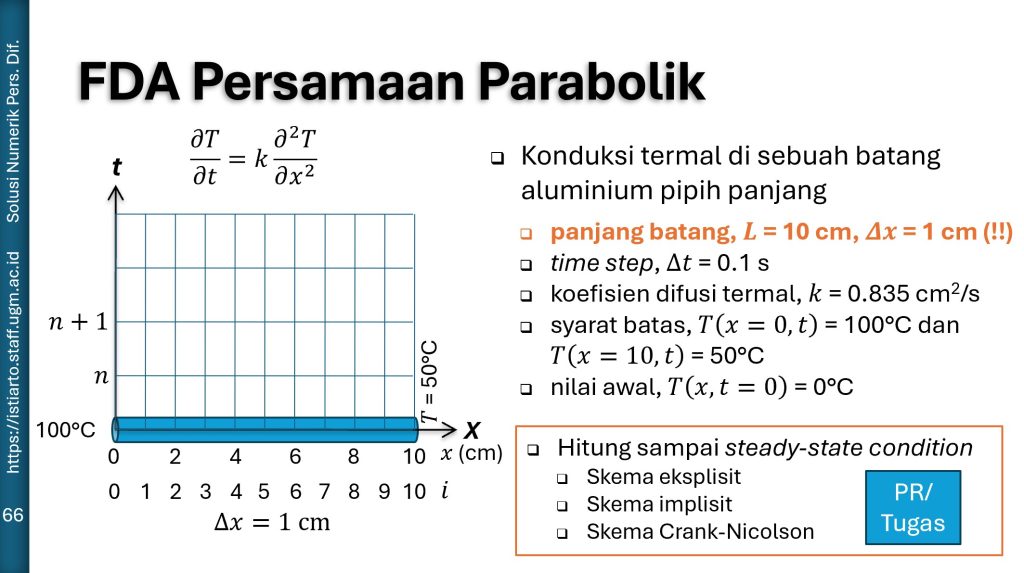
Metode Beda Hingga
import numpy as np
# difusi 1D, metode beda hingga, skema implisit
# noinspection PyShadowingNames
def algoritma_thomas(a, b, c, d):
n = len(d)
# matriks asli disimpan ke matriks baru, lokal di sini
cp = c.copy()
bp = b.copy()
dp = d.copy()
# forward sweep
for i in range(1, n):
m = a[i - 1] / bp[i - 1]
bp[i] = bp[i] - m * cp[i - 1]
dp[i] = dp[i] - m * dp[i - 1]
# back substitution
x = np.zeros(n)
x[-1] = dp[-1] / bp[-1]
for i in range(n - 2, -1, -1):
x[i] = (dp[i] - cp[i] * x[i + 1]) / bp[i]
return x
# data
panjang = 10.
k = 0.835
Delta_x = 1.
Delta_t = 0.1
jnode = int(panjang / Delta_x) - 1 # jumlah titik hitung
x = np.linspace(0, panjang, jnode + 2) # posisi titik dari pangkal x=0 s.d. ujung x=10 cm
# variabel skalar dalam contoh kuliah adalah T (temperatur)
# di program ini, variabel temperatur T diganti phi agar tidak rancu dengan variabel waktu t
# syarat awal
phi = np.zeros(jnode) # syarat awal, semua T = 0
# syarat batas
phi_batas_kiri = 100. # syarat batas di pangkal (kiri) T = 100
phi_batas_kanan = 50. # syarat batas di ujung (kanan) T = 50
# koefisien matriks sistem persamaan linear
aki = np.zeros(jnode - 1) # koefisien T_i-1
aka = np.zeros(jnode - 1) # koefisien T_i+1
ai = np.zeros(jnode) # koefisien T_i
rhs = np.zeros(jnode) # konstanta di sisi kanan =
# titik hitung ke-2 s.d. 1 dari batas kanan: i = 1, ..., jnode-2 (karena indeks di python mulai 0)
koef_ki = k * Delta_t / Delta_x / Delta_x
koef_ka = koef_ki
for i in range(1, len(ai) - 1):
aki[i - 1] = -1 * koef_ki
aka[i] = -1 * koef_ka
ai[i] = 1. + koef_ki + koef_ka
rhs[i] = phi[i]
# titik hitung pertama: i = 0 (node bertetangga dengan batas kiri)
i = 0
aka[i] = -1 * koef_ka
ai[i] = 1. + koef_ki + koef_ka
rhs[i] = phi[i] + koef_ki * phi_batas_kiri
# titik hitung paling kanan: i = jnode-1 (node bertetangga dengan batas kanan)
i = len(ai) - 1
aki[i - 1] = -1 * koef_ki
ai[i] = 1. + koef_ki + koef_ka
rhs[i] = phi[i] + koef_ka * phi_batas_kanan
# tulis judul kolom di baris pertama
tulis_teks = " ".join(f"{jarak:9.1f}" for jarak in x)
print(f" {tulis_teks}")
# iterasi phi[i] terhadap waktu t --> t+dt
t = 0.
tulis_teks = " ".join(f"{angka:9.4f}" for angka in phi)
print(f"{t:6.1f} {phi_batas_kiri:9.4f} {tulis_teks} {phi_batas_kanan:9.4f}")
for n in range(1, 201):
t = n * Delta_t
phi = algoritma_thomas(aki, ai, aka, rhs)
if (t % 1) == 0:
tulis_teks = " ".join(f"{angka:9.4f}" for angka in phi)
print(f"{t:6.1f} {phi_batas_kiri:9.4f} {tulis_teks} {phi_batas_kanan:9.4f}")
rhs[0] = phi[0] + koef_ki * phi_batas_kiri
for i in range(1, len(rhs) - 1):
rhs[i] = phi[i]
rhs[len(rhs) - 1] = phi[len(rhs) - 1] + koef_ka * phi_batas_kanan
print("selesai")
Metode Volume Hingga
import numpy as np
# TUGAS Makul SNPD
# Difusi 1D, skema implisit, metode volume hingga
# noinspection PyShadowingNames
def algoritma_thomas(a, b, c, d):
n = len(d)
# matriks asli disimpan ke matriks baru, lokal di sini
cp = c.copy()
bp = b.copy()
dp = d.copy()
# forward sweep
for i in range(1, n):
m = a[i - 1] / bp[i - 1]
bp[i] = bp[i] - m * cp[i - 1]
dp[i] = dp[i] - m * dp[i - 1]
# back substitution
x = np.zeros(n)
x[-1] = dp[-1] / bp[-1]
for i in range(n - 2, -1, -1):
x[i] = (dp[i] - cp[i] * x[i + 1]) / bp[i]
return x
# data
panjang = 10. # cm
Gamma = 0.835 # cm^2/s
Delta_x = 1. # cm
Delta_t = 0.1 # s
diameter = 0.6 # cm
luas = 0.25 * np.pi * diameter ** 2
Delta_V = luas * Delta_x
jmlvc = int(panjang / Delta_x) # jumlah volume kontrol
Delta_x = panjang / jmlvc # Delta_x dihitung ulang untuk penyesuaian dengan jumlah volume kontrol
x1 = np.arange(Delta_x/2, panjang, Delta_x) # jarak/posisi volume kontrol
x = np.concatenate(([0.], x1, [10.])) # jarak pangkal (x=0), volume kontrol, ujung (x=10)
# syarat awal
phi = np.zeros(jmlvc)
# syarat batas
phi_kiri = 100. # der C
phi_kanan = 50. # der C
# koefisien matriks tridiagonal
aW = np.zeros(jmlvc - 1) # diagonal bawah: jumlah koefisien adalah jumlah vk-1
aE = np.zeros(jmlvc - 1) # diagonal atas: jumlah koefisien adalah jumlah vk-1
aP = np.zeros(jmlvc) # diagonal utama: jumlah koefisien adalah jumlah vk
rhs = np.zeros(jmlvc) # konstanta di sisi kanan tanda kesamaan "="
# volume kontrol 2, 3, ..., jmlvc-1: i=1, 2, ..., jmlvc-2
koef_W = Gamma * luas * Delta_t / Delta_x / Delta_V
koef_E = koef_W
for i in range(1, jmlvc - 1):
aW[i - 1] = -1 * koef_W
aE[i] = -1 * koef_E
aP[i] = koef_W + koef_E + 1.
rhs[i] = phi[i]
# volume kontrol 1: i=0
koef_kiri = Gamma * luas * Delta_t / (Delta_x / 2) / Delta_V
aE[0] = -1 * koef_E
aP[0] = koef_kiri + koef_E + 1.
rhs[0] = phi[0] + koef_kiri * phi_kiri
# volume kontrol paling kanan: i=jmlvc-1
koef_kanan = Gamma * luas * Delta_t / (Delta_x / 2) / Delta_V
aW[jmlvc - 2] = -1 * koef_W
aP[jmlvc - 1] = koef_W + koef_kanan + 1.
rhs[jmlvc - 1] = phi[jmlvc - 1] + koef_kanan * phi_kanan
# iterasi phi[i] terhadap waktu t --> t+dt
t = 0.
tulis_teks = " ".join(f"{angka:9.1f}" for angka in x) # Mengubah angka x menjadi teks
print(f" {tulis_teks}") # Menuliskan posisi volume kontrol di baris pertama
tulis_teks = " ".join(f"{angka:9.4f}" for angka in phi) # Mengubah angka phi menjadi teks
print(f"{t:6.1f} {phi_kiri:9.4f} {tulis_teks} {phi_kanan:9.4f}") # Menuliskan nilai awal phi
for n in range(1, 201): # Menghitung phi pada waktu t+Delta_t
t = n * Delta_t
phi = algoritma_thomas(aW, aP, aE, rhs) # Penyelesaian persamaan linear, matriks tridiagonal
if (t % 1) == 0: # Mencetak hasil hitungan tiap detik
tulis_teks = " ".join(f"{angka:9.4f}" for angka in phi)
print(f"{t:6.1f} {phi_kiri:9.4f} {tulis_teks} {phi_kanan:9.4f}")
rhs[0] = phi[0] + koef_kiri * phi_kiri
for i in range(1, jmlvc - 1):
rhs[i] = phi[i]
rhs[jmlvc - 1] = phi[jmlvc - 1] + koef_kanan * phi_kanan
print("selesai")
HEC-HMS HEC-RAS SWMM
Saya memberikan pelatihan dalam kegiatan mini training di DTSL FT UGM berjudul “Aplikasi Perangkat Lunak Hidrologi-Hidraulika (HEC-HMS, HEC-RAS, SWMM) pada Kasus Drainase Kawasan Permukiman” pada 2021. Ini adalah one-day course, dilakukan secara daring. Materi yang saya samapkan adalah pengenalan dan contoh aplikasi HEC-HMS, HEC-RAS, SWMM untuk melakukan hitungan hidrologi dan hidraulika drainase kawasan. Saya mengajak peserta pelatihan untuk bersama-sama berpraktik menyusun model aliran drainase di sebuah kawasan permukiman hipotetik. Pelatihan menargetkan peserta akan mampu mengoperasikan HEC-HMS, HEC-RAS, dan SWMM untuk menransformasikan hujan menjadi limpasan langsung dan menyimulasikan aliran di saluran drainase sederhana.
Naskah modul pelatihan dapat diunduh di tautan berikut.
Aplikasi HEC-HMS HEC-RAS SWMM pada Drainase Kawasan Permukiman.
Pengaturan Format Bilangan Pecahan di Windows OS
Semua perangkat lunak aplikasi yang saya buat dan tayangkan di laman ini memakai titik “.”, bukan koma “,”, sebagai notasi atau tanda baca desimal bilangan pecahan. Cara mengatur notasi desimal di komputer atau laptop Windows adalah sebagai berikut.
Aktifkan “Settings”.
Pilih “Time & language”, kemudian klik “Language & region”.
Aktifkan “Administrative language settings” (menu ini ada di layar bagian bawah; scroll layar ke bawah untuk menampilkan menu ini).
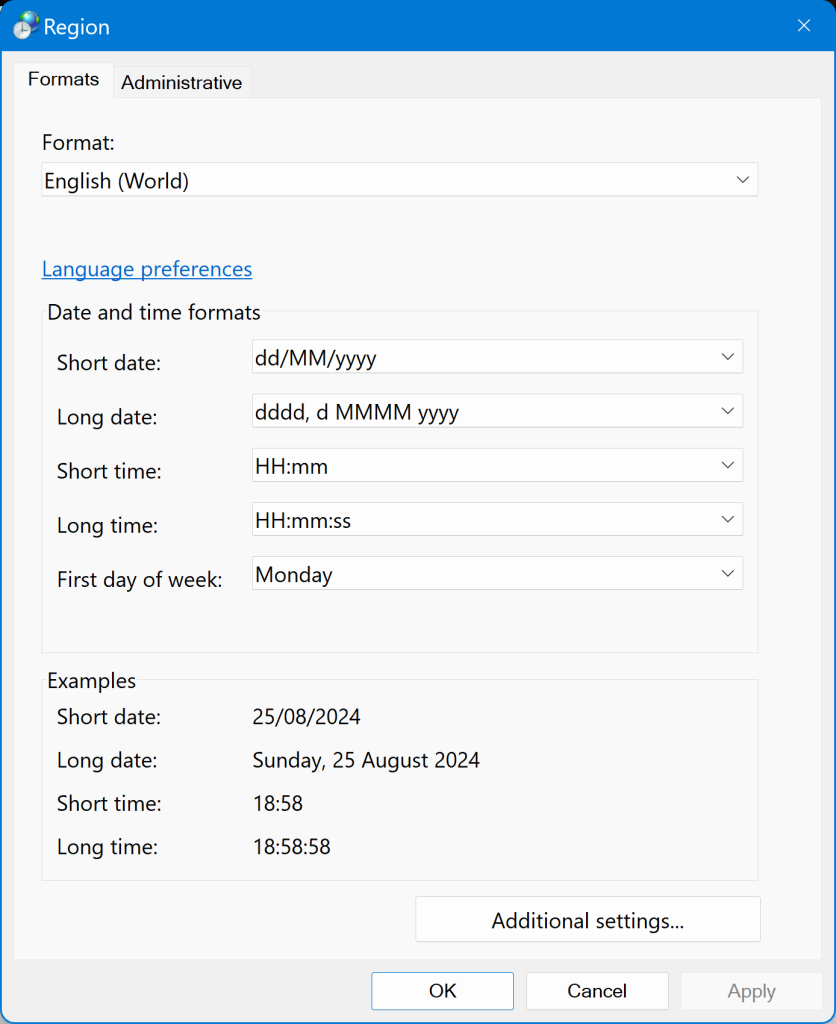
Aktifkan tab “Formats” di window Region yang muncul dan klik “Additional settings”.
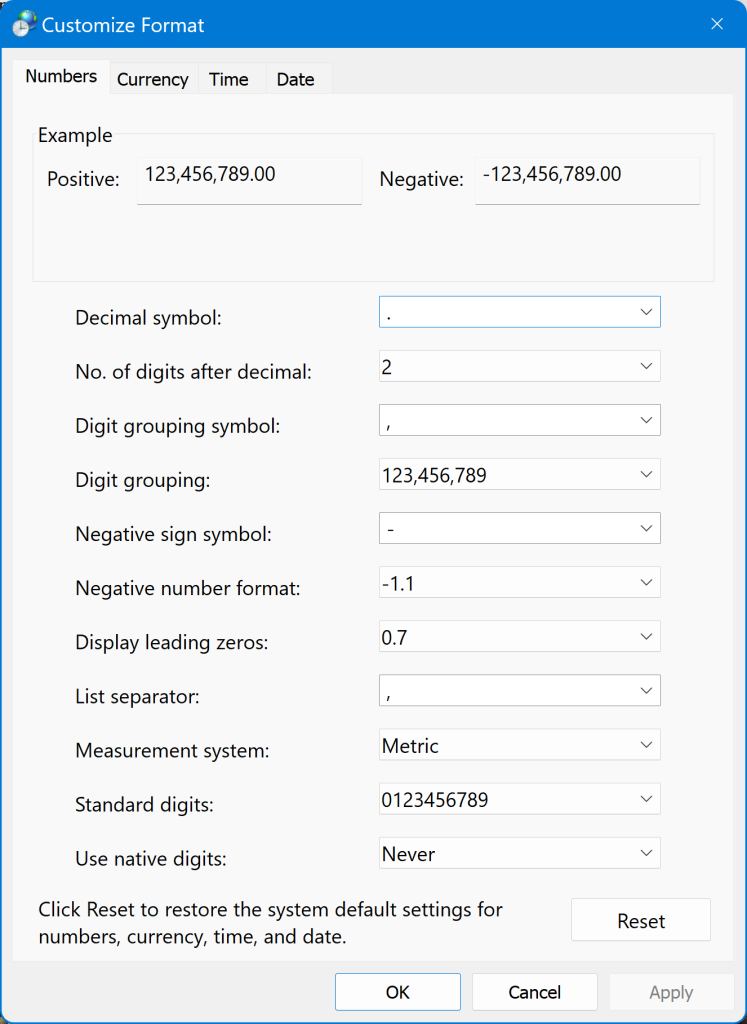
Aktifkan tab “Numbers” di window Customize Format yang muncul di layar.
Perhatikan isian “Decimal symbol”, pilih notasi titik “.”.
Dalam isian “Digit grouping symbol”, pilih notasi koma “,”.
Klik tombol “Apply”.
Klik tombol “OK” untuk menutup window.
HEC-RAS: Terowongan (Tunnel)
Saya mendapati beberapa simulasi aliran melalui sebuah terowongan (tunnel) yang dimodelkan sebagai gorong-gorong (culvert) dalam HEC-RAS. Ada cara lain untuk memodelkan terowongan, yaitu memodelkannya sebagai saluran (river station, RS) yang diberi tutup (lid).
Contoh, sebuah terowongan bertampang lintang trapesium di bagian bawah dan setengah lingkaran di bagian atas. Saluran bagian bawah dimodelkan sebagai saluran tampang trapesium seperti lazimnya saluran terbuka. Saluran bagian atas dimodelkan sebagai lid. Klik menu Option dari layar editor data tampang lintang (Cross Section Data), pilih submenu Add a Lid to XS. Data lid adalah koordinat (Station, High El., Low El.). High El. adalah elevasi muka tanah dan Low El. adalah elevasi langit-langit terowongan. Koordinat Station dan Low El., yang membentuk langit-langit terowongan setengah lingkaran, dapat dihitung di spreadsheet. Aktifkan Add a Preismann Slot. Klik tombol OK untuk menutup layar editor data lid dan kembali ke layar editor data RS.
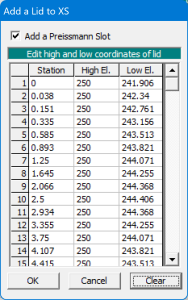
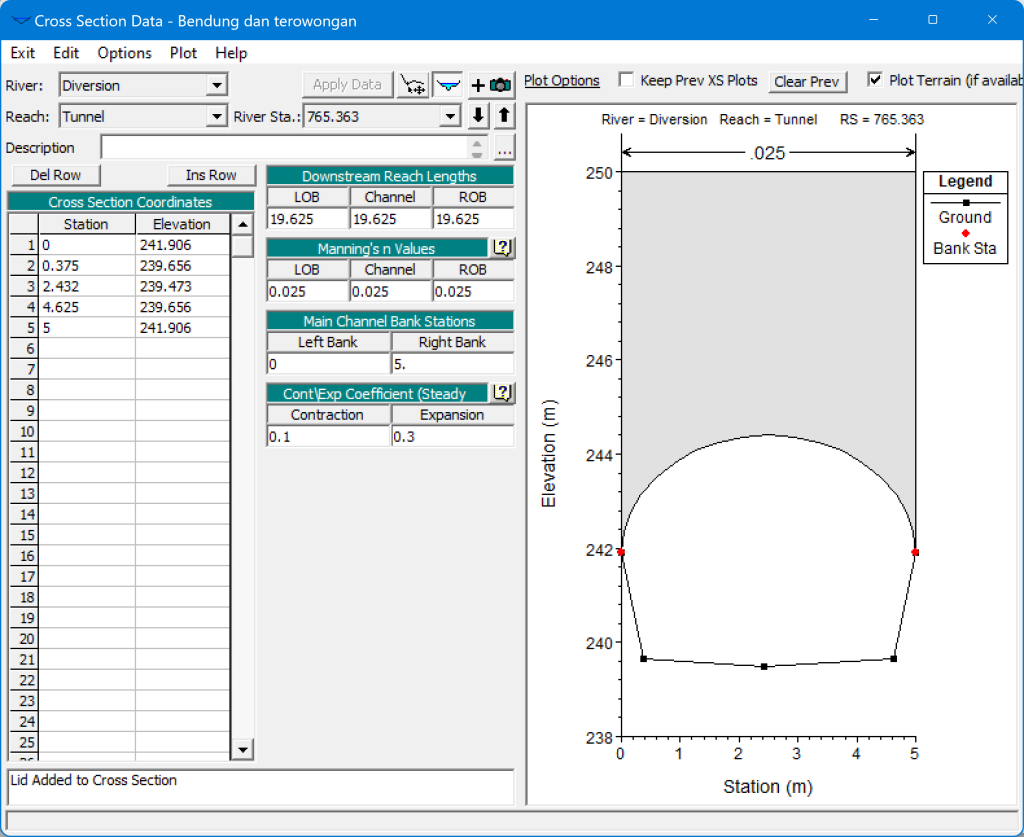
Terowongan dimodelkan sebagai river station yang memiliki tutup (lid).
Gambar di bawah ini adalah tampang memanjang terowongan setelah semua data RS yang membentuk terowongan selesai di-input-kan.

Tampang memanjang terowongan.
Page Not Found
Beberapa tautan di situs ini tidak bekerja. Kadang muncul pesan Not Found “Apologies, but the page you requested could not be found. Perhaps searching will help.” di layar Anda. Permasalahan ini disebabkan migrasi situs web ini dari platform WP ke platform WP Multi Site UGM. Upaya perbaikan tautan sedang dikerjakan secara bertahap. Mohon maaf atas ketidak-nyamanan ini.
Tabel Statistik
Saya mendapati kesulitan beberapa mahasiswa dalam membaca tabel-tabel statistik. Saya tayangkan tabel-tabel statistik yang telah saya ubah. Saya mengubah judul tabel dari judul berbahasa Inggris menjadi judul berbahasa Indonesia. Saya menambahkan pula keterangan dan contoh pemakaian tabel di bagian gambar sketsa kurva PDF. Semoga perubahan ini memudahkan mahasiswa dalam membaca tabel-tabel statistik.
Tabel distribusi normal standar
Tabel distribusi t
Tabel distribusi chi-kuadrat
Tabel distribusi F
Kursus HEC-RAS Maret 2020
Sejalan dengan upaya pengurangan risiko persebaran virus corona (covid-19), maka rencana penyelenggaraan kursus HEC-RAS Maret 2020 dibatalkan. Penyelenggaraan kursus serupa akan dijadwalkan setelah situasi kembali normal. Calon peserta yang telah mendaftarkan diri dimohon menghubungi Mbak Mukti (WA 08122967077) atau Mas Jaiz (WA 085643883363).
Pengukuran Transpor Sedimen
Kemarin ada pertanyaan kepada saya tentang cara pengukuran transpor sedimen di sungai. Saya tayangkan tulisan yang pernah saya buat sebagai bahan pelatihan tentang transpor sedimen di salah satu instansi pengelola sungai beberapa tahun yang lalu. Sila klik tautan di bawah ini.
HEC-RAS: Simulasi 1D-2D
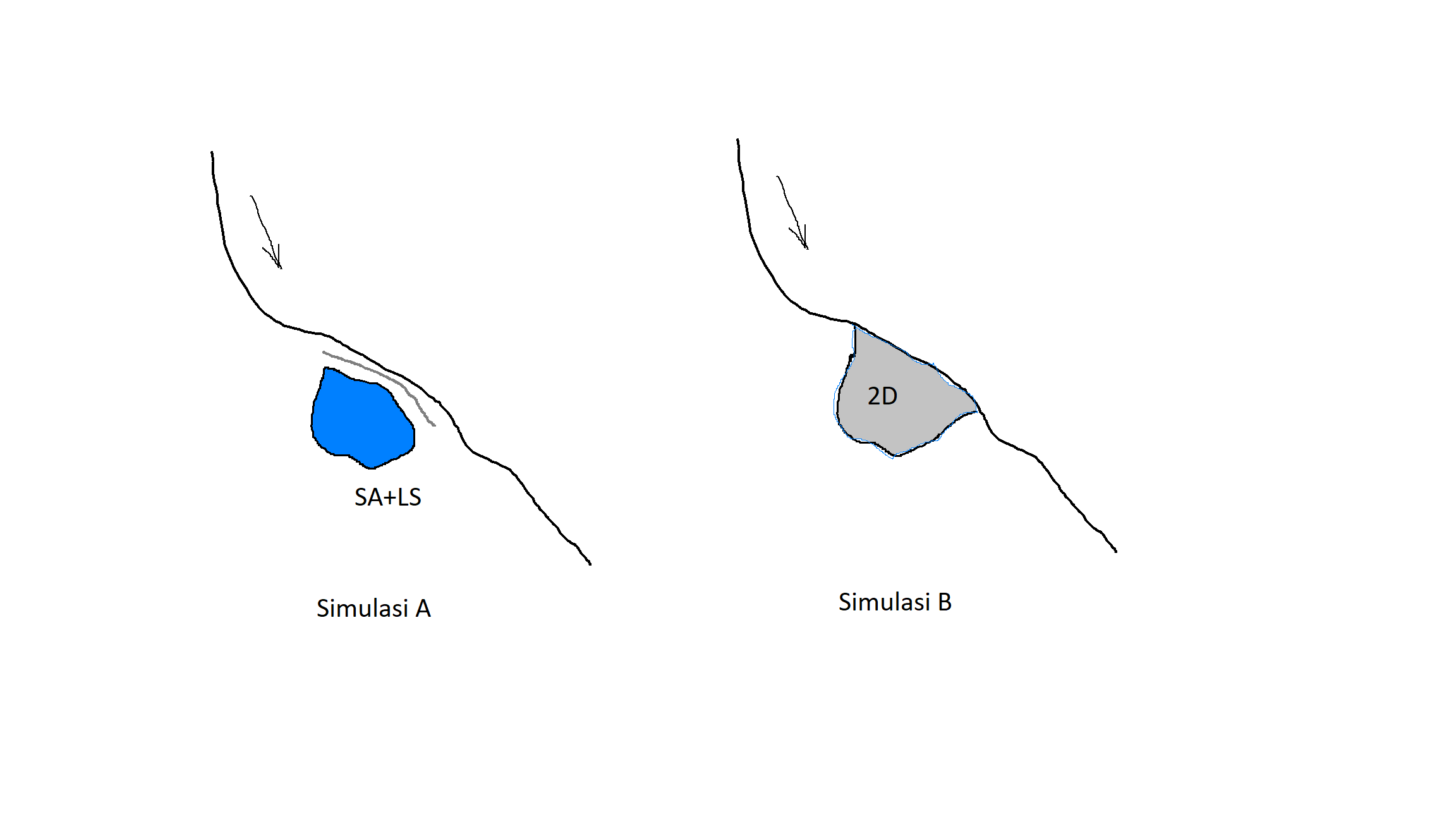
Melanjutkan tulisan saya mengenai fitur 2D dalam HEC-RAS, saya tunjukkan satu contoh pemakaiannya. Ketika di sebagian alur sungai yang kita modelkan terjadi limpasan keluar alur sungai, maka ada dua cara untuk memodelkannya. Simulasi A memakai fitur 1D: limpasan dimodelkan dengan lateral structure dan kawasan genangan dimodelkan sebagai storage area. Simulasi B memakai fitur 2D: limpasan dan genangan dimodelkan dengan fitur 2D, alur yang lain tetap dimodelkan dengan fitur 1D.
Perbedaan hasil dari kedua simulasi ini adalah bahwa Simulasi A memberikan hidrograf muka air dan debit aliran di storage area, tetapi tidak dapat memberikan kecepatan aliran di storage area. Simulasi B memberikan hasil berupa profil aliran (elevasi muka air dan kecepatan aliran) di setiap titik hitung di kawasan genangan. Simulasi B memberikan pergerakan aliran di kawasan genangan.